The Open Network (TON) is a Layer 1 blockchain that launched its mainnet in 2022. When TON prepared for their blockchain launch, they commissioned an audit from CertiK for all layers of the blockchain code: the node implementation, consensus engine, and smart contracts. In an audit, a human reviewer meticulously examines the source code line by line to ensure there are no mistakes. However, even the best auditors can miss subtle problems. Consequently, TON also commissioned formal verification of the key security properties of the two most critical smart contracts used in their blockchain implementation. Formal verification employs mathematical logic to confirm the code operates as intended. This formal verification discovered two subtle bugs, one of which could have resulted in a validator losing funds they had staked above the maximum allowed stake value.

Formal verification is performed by first drafting a security property in a computer-readable specification language, and then utilizing verification software to prove that the code fulfills that property under all possible circumstances. It differs from other forms of security review in two main ways. Firstly, the security properties are mathematically precise, avoiding the potential vagueness or ambiguity of English-language descriptions. Second, in contrast to other assurance methods like testing or manual code review, there is no risk of accidentally overlooking some rare situation in which the security property is violated.
This is the second in a series on formal verification of the whole Web3 stack. The first post looked at the formal verification of Ant Group's HyperEnclave TEE.
For TON, we verified two smart contracts—elector and config—which are essential for maintaining key parts of the blockchain state. These contracts manage the consensus state in the blockchain implementation. The config contract oversees the updating of the chain's configuration registers, including the current set of validators. The elector contract implements the staking algorithm: it receives bids from users wishing to become validators in the subsequent period, selects the highest bidders, locks up their funds, and then transmits the chosen set of validators to config. When we embarked on the formal verification, both contracts had already been manually audited. In this blog post, we detail the verification of the elector contract; information about the config contract is available in the full audit report.
The Program
The elector contract implements several functions: staking, election of validators, complaints (voted on by the current validator set), and code upgrades. In the verification, we examined the staking/election cycle and did not investigate complaints or upgrades.
The staking/election cycle is instrumental in selecting a set of validators who subsequently assume responsibility for maintaining blockchain consensus over the next period. During the election period, any user can send a bid to become a validator, prompting the contract to lock up the corresponding funds. Upon the election period's conclusion, the top 'n' bidders are chosen as validators and their stakes remain locked, while the losing bids are eligible for a refund. An error in this contract could potentially compromise the blockchain's integrity—if someone could ascend to the role of a validator without a valid stake—or endanger the funds of the participants—if funds could either be drained from the contract by an attacker, or become permanently locked within it.
The contract's full source code is available on GitHub. It is written in FunC, a programming language specific to the TON blockchain. Below is a summary of its functionality.
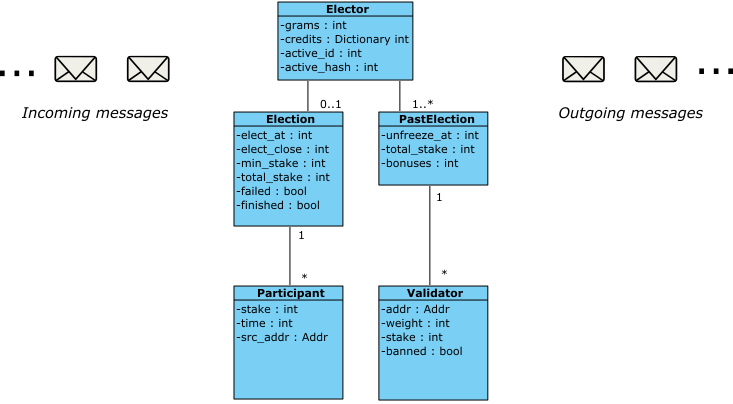
The contract manages key state variables such as: cur_elect, a dictionary tracking each user's stake in the current election; finished, a boolean indicating whether the election is still in progress; and past_elections, a record of the election dictionaries from previous elections that are now considered "frozen"—i.e., they will not undergo further modifications. Notably, one of these frozen dictionaries records the funds staked in the immediately preceding election, which dictated the currently established validator set.
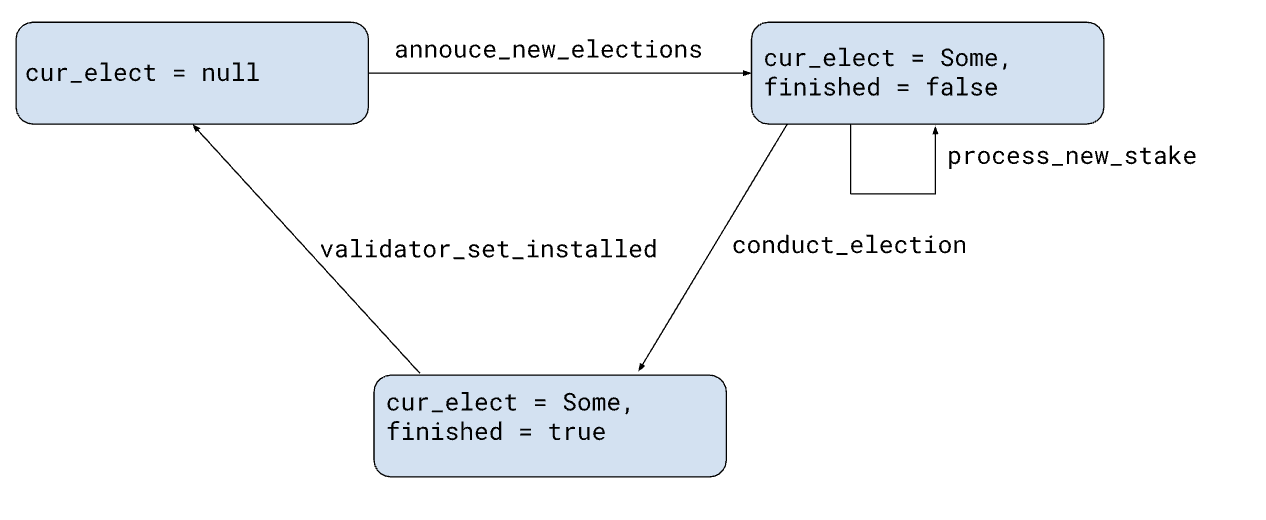
The diagram above illustrates the evolution of this state during the staking/election cycle. Once per block, a function run_ticktock in the contract is invoked. This function in turn calls announce_new_elections, conduct_election, and validator_set_installed, each transitioning to a new state if the appropriate conditions are met. In the initial state, the cur_elect field of the contract state is set to null. At a certain point, the function announce_new_elections determines the commencement of a new election period and updates the cur_elect field to reflect the beginning of the election. It also retrieves relevant data from the next validator set, stored as part of the contract's configuration parameters, to calculate the active duration of this election, subsequently storing it within the election. Upon completion, it alters the contract's state to indicate an ongoing election.
While the election is in progress, users submit new stake requests (managed by the process_new_stake function) to register their bids for the current election.
Once the current time exceeds the value in the elect_close field of the election, the conduct_elections function sets the finished flag to true, updates the current validator set to the set designated as the next validator set, and adds the current election to the past_elects dictionary under the elect_at key acquired from the election.
After this is done, the validator_set_installed function modifies the state so that there is no ongoing election (i.e., it resets the cur_elect field to null), and updates the active_id stored in the state to the ID of the new validator set.
At any given moment, the functions process_simple_transfer and process_new_stake can be called to allow a participant to increase their stake in a particular election (this is rejected if no election is ongoing) and to transfer value to the contract, either as a bonus to one of the elections or to the amount stored in the contract respectively. Furthermore, a user can invoke recover_stake at any time to reclaim stakes from past elections that have already been unlocked.
The Correctness Property
Formal verification entails proving that a model of the program satisfies a declared property, both of which necessitate careful examination to fully understand the proven guarantees. First, let's contemplate the property we want to prove about the elector contract.
Crafting correctness properties for a program demands creativity and discernment. These properties should be succinct and easy to comprehend. Lengthy statements that merely recapitulate the program's logic ("after calling this method, the variables will have these specific values...") risk transferring bugs from the code to the specification. If we're only verifying sections of the code, then the correctness properties should pertain to parts relatively likely to contain errors. Additionally, the properties should offer meaningful security assurances to the end-user.
Regarding the elector contract, there are multiple different properties that should be valid. For instance, the selected users should genuinely be the highest bidders, the communication with the config contract should adhere to the intended protocol, and so forth. Ultimately, we chose to prove an accounting invariant, which also infers a lower limit on the locked funds.
As the election process unfolds, users send funds to, or withdraw funds from, the contract. This contract manages several data structures (as illustrated in the diagram below) to keep track of received funds and their sources. Specifically, there is a stake for each participant in the current election, a stake for each validator from past elections, and a grams field denoting funds owned by the contract itself (utilized to cover gas costs). The invariant states that if you aggregate all these figures, they equate to the difference between the total amount dispatched to the contract and that dispatched from the contract. In simpler terms, all incoming funds are correctly accounted for.
This invariant is straightforward to state. We formulate a "contract value" that aggregates all the figures in the contract, specifically:
(sum of the current elections dict) + (sum of values in all the frozen election dicts) + (sum of credits) + grams + (sum of values in the outbox of messages)
The invariant then asserts that the actual funds present in the contract (the difference between incoming and outgoing transfers) are at least equivalent to what is documented. (In truth, they are precisely equal, but in our contract model, we overlooked the deduction of gas costs for dispatching some messages, hence we only prove an inequality).
Definition contract_value (r : RData) : Integer := (match (cur_elect r) with | Some elect => CurElections_value elect | None => 0) + sum_with PastElections_value (past_elects r) + sum_with id (credits r) + grams r + sum_of_value (outputs r) end. Definition credits_invariant (st : TON_state) : Prop := let (to_contract, from_contract) := List.partition (fun m => Addr_eqb elector_addr (addr (snd m))) (ton_messages st) in sum_of_value (List.map snd to_contract) >= contract_value (elector_state st) + sum_of_value (List.map snd from_contract).
The invariant is likely to reveal bugs since nearly all the methods involved in the election cycle manage staked funds in some capacity, necessitating the return of it to the user or its recording in the data structures. For instance, failure to address a specific type of message could potentially violate the invariant. Also, proving this property will compel the proof engineer to consider all the control flow paths in the program, so even without a violation of the invariant, we might still identify bugs.
Finally, the invariant enables us to validate two security properties pertinent to the end user. First, it ensures that the contract will never deplete its funds: whenever a function attempts to send a message with a specific value (e.g., reimbursing a stake to a user), the operation will never fail due to insufficient value in the contract.
Second, the contract value encompasses the "frozen" dictionary which tracks the stakes of the current set of validators from the previous election, and it will only release these funds and install a new set if a minimum of MIN_STAKE (a configuration parameter) has been committed. This allows us to affirm that the contract value is at least MIN_STAKE. Together with the accounting invariant, this represents a security property that is meaningful for the end user: it verifies that the set of validators have always secured the minimum required stake.
Modeling the Program
To perform verification on a program, it must first be converted into a format that verification tools can process. Generally, this means translating it into a unique programming language supported by the tool. In this context, we utilize the Coq Proof Assistant, which offers both a programming language and a means to declare and prove theorems about programs in that language. Hence, the initial step is to translate FunC into Coq's built-in language.
Given that this was our first time verifying a FunC program, we performed the translation manually. We scrutinized the functions line by line and drafted corresponding functions in Coq. If verifying FunC becomes a recurring task, we would contemplate developing a tool to automate such a translation to conserve time and enhance reliability. The proof pertains to the modeled code and not the original FunC source, so if we made any transcription errors, we could, theoretically, miss a bug.
The translated program typically operates at the same abstraction level as the original FunC. However, we made two simplifications. First, the original employs 257-bit signed integers, but in our translated code, we use unbounded integers. Second, the original code avoids using struct types, instead employing standard library functions to pack/unpack values into memory cells, whereas we use structs or tuples in the translated code. For instance, when the original code uses begin_cell / store_uint to construct a 3-element tuple:
sdict~dict_set_builder(128 + 32 + 256, key, begin_cell() .store_uint(min(max_factor, max_stake_factor), 32) .store_uint(addr, 256) .store_uint(adnl_addr, 256));
…we just make one directly:
set key (min max_stake_factor max_factor, addr, adnl_addr) st.
The two simplifications serve to diminish the proof effort by limiting the scope of the verification. To prove that overflows do not occur would necessitate tracking numerous extra assumptions about the range each variable can assume. Regardless, the accounting invariant is a "safety property", suggesting that any state that can be reached satisfies it. Thus, even if a call to the contract was terminated due to an overflow error, the invariant would still hold true (such a failed call doesn't lead to a new state).
Similarly, using an in-depth model of struct packing/unpacking would compel the proof to include a considerable number of assumptions about the intended types of stored values. While feasible, it doesn't significantly increase assurance beyond carefully inspecting each site during translation. The meticulous examination by a proof checker is more effectively employed to verify more nuanced global invariants.
In the actual blockchain, the contract's functions reside in a broader environment. They are compiled to bytecode, which is interpreted on the blockchain nodes and executed in response to requests from other computers. In this verification, that environment is abstracted into just a few lines of code that say the contract function is called and updates the contract state. We still require some assumptions: primarily, that the MIN_STAKE configuration parameter remains at a fixed value, ensuring that the contract locks up at least that much.
The Proof
After these preliminaries and caveats, what does the actual proof consist of? It necessitates contemplating every conceivable control flow path within each function in the contract, and establishing that upon the function's completion, the contract resides in a state that aligns with the invariant. While this is routine work for some functions, those that contain loops, in particular, call for more input from the proof engineer. This is because these loops cannot simply be stepped through mechanically.
Take the contract's most extensive function, try_elect, as an example. With its 110 lines and 5 loops, its verification necessitates labelling each of these loops with distinct identifiers such as add_participants, participants_to_list, remove_i_elements, and stake_total. For each loop, the proof engineer must concoct a postcondition, a robust condition that reflects the expected state of the contract when the loop concludes, to assist in proving the final theorem. Additionally, the engineer must develop a robust invariant, a condition regarding the contract's state during the loop's execution, to validate that postcondition.
As an illustration, consider a do-loop in this function that calculates the total stake for the upcoming elector set.
... ;; l is the list of all stakes in decreasing order int i = min_validators - 1; var l1 = l; repeat (i) { ;; remove_i_elements l1 = cdr(l1); } var (best_stake, m) = (0, 0); do { ;; stake_total var stake = l1~list_next().at(0); i += 1; if (stake >= min_stake) { var tot_stake = compute_total_stake(l, i, stake); if (tot_stake > best_stake) { (best_stake, m) = (tot_stake, i); } } } until (i >= n); if ((m == 0) | (best_stake < min_total_stake)) { return (credits, new_dict(), 0, new_dict(), 0, 0); } ...
One of the properties we substantiate is a lemma stipulating that, upon the loop's completion, the computed best_stake originates from a call to the compute_total_stake auxiliary function, or from a previous cycle of the loop.
Lemma last_call_compute : forall iter (min_stake i best_stake m numValidators total_participants : Integer) (all_elem : v_list) (r r': RData) m_stake m_stake' tot_stake, stake_total min_stake i best_stake m total_participants m_stake' all_elem iter r = Some (tot_stake, numValidators, m_stake, r') -> compute_total_stake_spec all_elem numValidators m_stake r = Some (tot_stake, r') \/ (tot_stake = best_stake /\ m_stake = m_stake' /\ m = numValidators /\ r = r').
The lemma is articulated in Coq's specification language and alludes to the function stake_total, the moniker we attributed to this specific loop in the translated FunC program. The lemma employs conventional logical notation: for any inputs to stake_total (forall), if the function returns a pair Some (tot_stake, r’) then that entails (->) that one of two conditions is met (logical or \/). To convince the proof assistant of this statement's veracity, we composed a “proof script” (not pictured above), which for this lemma encompasses 22 succinct lines of commands that steer Coq through evaluating how the function computes for all possible inputs.
Bugs Discovered
The process of verification brought to light two instances in the code where the accounting invariant was compromised. The first instance is rather minor: a variable is employed to track the contract's own funds for its operations, particularly to cover the costs of messaging other contracts. However, in one instance, this variable was not deducted upon message transmission, leading to a marginally inaccurate current balance.
The second instance is decidedly more critical. It is located in the function that accommodates new bids (process_new_stake), which is designed to lock the appropriate amount of funds within the contract, and to refund any excess to the user. However, this function does not detect if a user inadvertently submits a bid that exceeds the configuration parameter max_stake. Subsequently, during the election procedure, the contract will inconspicuously disregard the excess funds in the bid. Consequently, these surplus funds become indefinitely locked within the contract, and are irrevocably lost to the user.
This error is notably challenging for a human to detect. It is confined to a single line within the 110-line try_elect function, embedded within a function that formulates a list l of bids.
... var l = nil; do { var (key, cs, f) = sdict~dict::delete_get_min(128 + 32 + 256); if (f) { var (stake, _, pubkey) = (min(key~load_uint(128), max_stake), key~load_uint(32), key.preload_uint(256)); ;;<-- problem here. var (max_f, _, adnl_addr) = (cs~load_uint(32), cs~load_uint(256), cs.preload_uint(256)); l = cons([stake, max_f, pubkey, adnl_addr], l); } } until (~ f); ...
The expression min(key~load_uint(128), max_stake) diminishes the stake value down to max_stake without retaining the former value. However, since it's intermingled with the code to convert from a map to a list, its connection to the tracking of received funds in the contract isn't immediately apparent. This code had been scrutinized by both the development team and our manual audit, yet none of the reviewers identified this discrepancy.
In contrast, for the formal verification process to proceed, we must prove a postcondition asserting that all the bids previously logged in the map are now recorded in the list. While doing so, it becomes evident that we require an additional presumption about the min operation. In our lemma, this assumption manifests as the hypothesis that stake = min stake max_stake:
Lemma list_elem_exist : forall (members : Dict Participant) (st : p_info) (max_stake : Integer), (forall key stake time max_factor addr adnl_addr, get key members = Some (mkParticipant stake time max_factor addr adnl_addr) -> (stake = min stake max_stake)) -> (forall key stake time max_factor addr adnl_addr, get key members = Some (mkParticipant stake time max_factor addr adnl_addr) -> exists mx, get (tup_to_int (stake, -time, key)) st = Some (mx, addr, adnl_addr))-> mem_to_list members (participants_to_list max_stake st).
In order to pinpoint this issue, one must trace the complete flow of funds from the process_new_stake function, through the election's members field in the contract, the l intermediate list in the try_elect function, and finally to the definitive dictionary of locked stakes. This precise line of reasoning is where formal verification truly shines.
Conclusions
The formal verification of the elector and config contracts demonstrates their adherence to specific properties related to staking and accurate vote counting.
Given that formal verification constitutes only a portion of the complete audit, it is also beneficial to compare it with the manual audit report for the corresponding code. It is evident that there are numerous findings about the overarching design, economics, and coding style, which fall outside the scope of the formal properties we analyzed. Yet, even after such manual review, formal verification was able to unveil violations of the intended invariant. For the highest degree of confidence in critical code, a combination of formal verification and manual auditing should be utilized.



